HyDE 是由CMU的 Luyu Gao (主页: https://luyug.github.io/ ) 等人于2022年12月在论文《Precise Zero-Shot Dense Retrieval without Relevance Labels》中提出的一种RAG 查询优化算法。

原理

HyDE 是一种查询改写技术。 在标准的 RAG 实现中， 向量检索 (Deep Retrieval) 所使用的Query是原始查询字符串的 Embedding向量。 在实际应用场景中， 原始查询与真实答案Embedding的相关性可能没有被向量语义空间很好地捕捉， 比如在 QA (问答) 场景中使用了基于语义相似性训练的向量模型。 这时， 直接原始问题进行相似性查询得到的更可能是与原问题在语义上相似的文档片段， 而并不能回答原始问题。 另一方面， 用户的查询可能包含较大的噪声， 直接进行 Embedding 会导致检索到较多不相关的结果 。

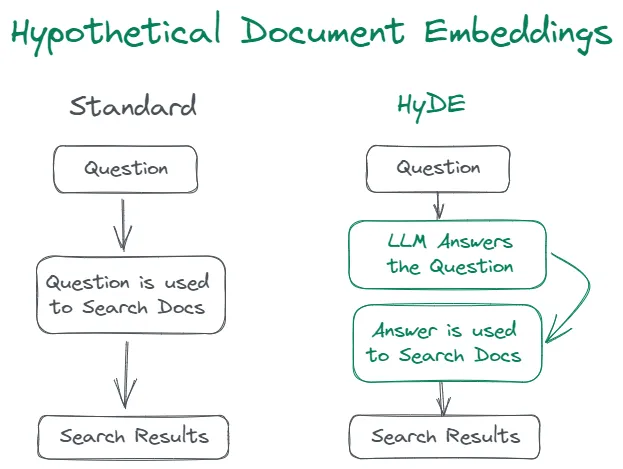
HyDE的思想非常简单直接: 对于给定的用户查询 Query, HyDE 先通过LLM生成假设的回答，这些假设性的回答称为 Hypothetical Document (假设性文档), 由于缺少领域性、时效性的知识以及模型幻觉问题的存在， 这些假设性答案通常不正确的， 但与原问题相比， 它们在语义上与真实的相关文档更加接近。下一步则是将这些假设性文档进行Embedding向量化，再通过近似近邻检索(ANN)找到最相关的K个向量。 如下图示:

如果大家做过推荐算法， 很快就会发现 HyDE 不过是 i2i 算法在 RAG 场景的简单推广。 在推荐算法中， 为了召回用户可能感兴趣的商品， 我们通常并不使用用户的 Embedding（难以训练而且成本较高）, 而是拿到用户过去有过正反馈行为的商品， 再通过商品的 Embedding 来检索其相关的商品作为推荐给用户的候选商品。

实现

与标准RAG相比， HyDE的核心操作是生成假设性文档， 并得到改写后的查询向量。

生成假设性文档可以直接调用LLM实现， Prompt可以根据场景自定义， 比如:

1
2
3
Please write a passage to answer the question
Question: {question}
Passage:

假设通过LLM生成了$N$ ($N >= 1$)个假设性文档, 有两种方法得到最终的查询向量:

一是直接对这N个查询文档的向量进行平均, 即:
$$
v=\frac{1}{k}\left[\sum_{i = 1}^{k}f(d_{i})\right]
$$
另一种方法是将原始的查询向量也作为一个假设性文档， 即:

$$
v=\frac{1}{k + 1}\left[\sum_{i = 1}^{k}f(d_{i})+f(q)\right]
$$

在论文中， 作者宣称， 与当时的SOTA无监督向量检索算法 Contriver 相比， HyDE能够大幅提升 RAG 检索性能， 在 Web 搜索、QA、事实核查等任务中达到了有监督微调算法同等的性能。